CONJUNTOS

 

Conjunto é o conceito da reunião de elementos com algum aspecto em comum, como é o caso do conjunto de policiais de uma delegacia. Os elementos estão reunidos com um objetivo comum.

 

O conjunto é representado por uma letra maiúscula, enquanto os seus elementos são representados por letras minúsculas.

 

Para relacionar um elemento com um conjunto deve-se usar o símbolo de pertinência: Î (pertence) ou Ï (não pertence).

 

     

Exemplo:

 

    Sendo o conjunto:  A = {1, 2, 3, 5, 7, 8},   temos que   2  Π A    e    4  Ï A.

 

 

SUBCONJUNTOS

 

 

     Os símbolos Ì (está contido), Ë (não está contido), É (contém), e    (não contém) são usados para relacionar dois conjuntos, sobretudo para indicar se um conjunto é subconjunto do outro.

 

Exemplo:

      Sendo os conjuntos:   A = {x/x é letra do alfabeto}  e   B = {a, e, i, o u}, temos  que  B  Ì  A, pois B é subconjunto de A, haja vista que todos os elementos do conjunto B pertencem ao conjunto A.

 

REPRESENTAÇÃO

 

      Pode-se usar a representação por extensão ou notação explícita, pois os elementos são exibidos entre chaves, separados por vírgulas. Pode-se também usar a representação por compreensão ou notação implícita, quando descrevemos os elementos que atendam ao conjunto dado.

 

Exemplo:

            A = {0, 2, 4, 6, 8} ® extensão

            A = {x Î N / x é número par menor que 10} ® compreensão

 

DIAGRAMA DE VENN:  É uma representação geométrica, podendo ser utilizada qualquer figura. O usual é a forma ovalada abaixo:

 

 

           

 

                                    ou seja,    A = {1, 2, 3}                      

 

 

     

      O diagrama também pode assumir outras formas geométricas:

   

 

 TIPOS DE CONJUNTOS

 

Conjunto Vazio: existem conjuntos que, por alguma situação específica, não têm elementos. Esses são os conjuntos vazios, representados por {  }  ou Æ.

 

Exemplo: Conjunto dos números ímpares menores que um   ®   A = Æ    ou   A =  {   }

 

Conjunto Unitário: possui um único elemento.

 

Exemplo: Conjunto de números primos pares  ®  A  =  { 2 }

 

Conjunto Finito: tem um número determinado de elementos.

 

Exemplo: A = { x / x é candidato do concurso público de uma turma}

 

Conjunto Infinito: tem um número indeterminado de elementos.

 

Exemplo: Todos os números maiores que 5 ®  A = { 6, 7, 8, 9, 10, 11, 12, 13, 14 ...}

 

 

OPERAÇÕES COM CONJUNTOS

 

União de conjuntos  (È):   a união de dois conjuntos A e B é o conjunto formado por todos os elementos que pertencem a A e a B juntos.

 

Exemplo:  A = { 0, 1, 2, 3, 4, 5}  e  B = { 2, 4, 6}

 

 

Interseção de conjuntos  (Ç): a intercessão de dois conjuntos A e B é o conjunto formado pelos elementos que pertencem a A e a B ao mesmo tempo.

 

Exemplo: A = {0, 1, 2, 3, 4, 5}  e  B = {2, 4, 6}

 

 

 

 

 

Diferença de conjuntos  (-) : a diferença de dois conjuntos A e B é o conjunto formado pelos elementos que pertencem a A mas não pertencem a B.

 

Exemplo:  A = {0, 1, 2, 3, 4, 5}  e  B = {2, 4, 6}

 

 

Complementar de B em relação a A: o complementar de B com relação a A é o que falta para o B ficar igual ao A.

 

Pode-se resolver problemas de conjuntos fazendo a interpretação adequada e utilizando, para a resolução, os Diagramas de Venn, associados às operações com conjuntos.

Exemplo:

 

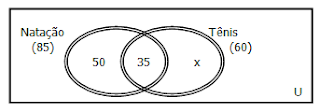
Um clube oferece, a seus associados, aulas de natação e tênis. Encerradas as inscrições, verificou-se que dos 85 inscritos em natação, 50 só farão natação; o total de inscritos para as aulas de tênis foi 60. Calcule o número de associados que se inscreveram somente para as aulas de tênis.

 

 

 

 

Observe que o número total de inscritos em natação é 85, como o número dos que fazem só natação é 50, faltam 35 para se encaixarem na região da interseção (inscritos nos dois esportes). Já existem no diagrama 35 inscritos em tênis, faltando, então, 25 para ocuparem o lugar do x (inscreveram-se somente para tênis).  U é o conjunto universo, no qual estão contidos os outros conjuntos.

 

Resposta: 25 inscritos somente em tênis.

 

 

OS PRINCIPAIS CONJUNTOS

 

Conjunto dos números naturais  ¾ N:   É natural todo número inteiro e positivo.

 

N  =   { 0, 1, 2, 3, 4, 5, 6, 7 ...}

N* =  {1, 2, 3, 4, 5, 6, ...}   ®    o asterisco indica a exclusão do zero

 

Conjunto dos números inteiros  ¾  Z: Podem ser positivos, negativos ou zero, como elemento central, na reta numérica.

 

 

Z  =  { ... –3,  –2, –1,  0,  1,  2,  3 ...}

Z₊ = { 0, 1, 2, 3, 4, 5 ...} ®  não-negativos

Z _- = { 0, -1, -2, -3, -4, ...} ®  não-positivos

 

Observação: O oposto ou simétrico do número  2  é  –2 , de  –5  é  5, e assim por diante.